Διάταξη:

• Παλμογεννήτρια
• Πηνίο με συντελεστή αυτεπαγωγής 44mH
• Πυκνωτής χωρητικότητας 10 μF
• Αντίσταση 100 Ω
• Παλμογράφος Δυο Καναλιών

Διαδικασία:

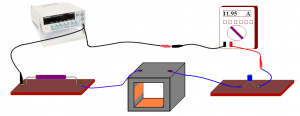
Συνδέουμε σε σειρά την αντίσταση, το πηνίο, το πυκνωτή και το τροφοδοτικό εναλλασσόμενης τάσης. Συνδέουμε το αμπερόμετρο σε σειρά μετά το πηνίο του κυκλώματος. Τροφοδοτούμε το κύκλωμα με ημιτονοειδές σήμα συχνότητας 200 ως 300 Hzμε την βοήθεια της παλμογεννήτριας. Μεταβάλλουμε την συχνότητα της παλμογεννήτριας και προσέχουμε την οθόνη του αμπερόμετρου. Παρατηρούμε ότι η τιμή του ρεύματος που διαρρέει το κύκλωμα για κάποια δεδομένη συχνότητα λαμβάνει μέγιστη τιμή και μετά μειώνεται. Γιατί συμβαίνει αυτό;

Εξήγηση:

Ας θεωρήσουμε ότι η παλμογεννήτρια μας, μας τροφοδοτεί με ημιτονοειδές σήμα της μορφής  $V=V_{0}\eta\mu\omega t$. Η συνολική διαφορά δυναμικού V_Σ είναι το άθροισμα της διαφοράς δυναμικού στα άκρα της αντίστασης V_R, της διαφοράς δυναμικού στα άκρα του πηνίου V_Lκαι της διαφοράς δυναμικού στα άκρα του πυκνωτή V_C. Όπως έχουμε δει είναι:$V_{R}=I_{0}R\eta\mu\omega t$

$V_{L}=I_{0}Lω η\mu(ω t+\frac{\pi}{2})=I_{0}Lω σ υ ν ω t$

$V_{C}=\frac{I_{0}}{ω C}η\mu(ω t-\frac{\pi}{2})=-\frac{I_{0}}{ω C}σ υ νω t$

άρα είναι:

$V_{Σ }=V_{R}+V_{L}+V_{C}=I_{0}Rη\mu(ω t)+Ι _{0}(Lω -\frac{1}{ω C})σ υ ν(ω t)=Ι _{0}R(η\mu
(ω t)+\frac{Lω -\frac{1}{ω C}}{R}σ υ ν(ω t))=$

$I_{0}R(η\mu(ω t)+\tan φ σ υ ν (ω t))=I_{0}R\frac{η\mu(ω t+φ )}{σ υ ν φ }=I_{0}R\frac{η\mu(ω t+φ )}{\frac{R}{\sqrt{R^{2}+(Lω -\frac{1}{ω C})^{2}}}}\Rightarrow I_{0}Zη\mu(ω t+φ )$

όπου $Z=\sqrt{R^{2}+(Lω -\frac{1}{ω C})^{2}}$

είναι η σύνθετη αντίσταση ή εμπέδηση του κυκλώματος και εκφράζεται σε Ohms.

Το μέγιστο ρεύμα που παρατηρούμε στο αμπερόμετρο μας οφείλεται λόγω του φαινομένου του συντονισμού. Ένα κύκλωμα βρίσκεται σε κατάσταση συντονισμού όταν η σύνθετη αντίσταση του κυκλώματος είναι ίση με την ωμική αντίσταση R.

Στο κύκλωμα μας, δηλαδή όταν: $Z=R\Rightarrow\sqrt{R^{2}+(Lω -\frac{1}{ω C})^{2}}=R\Rightarrow
Lω =\frac{1}{ω C}\Rightarrow ω _{0}=\frac{1}{\sqrt{LC}}$ Άρα η συχνότητα συντονισμού είναι: $f₀=(1/2π√LC)$ και σύμφωνα με τα χαρακτηριστικά των εξαρτημάτων του κυκλώματος μας είναι $f_{0}^{θ ε ω ρ }=\frac{1}{2\pi\sqrt{LC}}=\frac{1}{2\pi\sqrt{44\ast10^{-3}10\ast10^{-6}}}=240Hz$.

Όμως κατά την διάρκεια εκτέλεσης του πειράματος μας είδαμε στην οθόνη του αμπερόμετρου μας ότι το ρεύμα αυξάνεται σε μια συχνότητα κοντά στα 280 Hz. Αυτό συμβαίνει γιατί αφενός το πηνίο μας δεν είναι ιδανικό αλλά έχει κάποια εσωτερική αντίσταση και αφετέρου το αρχικό πηνίο προσδίδει στο κύκλωμα μας μια επιπλέον εμπέδηση.