Διάταξη:

• Παλμογεννήτρια
• Πηνίο με συντελεστή αυτεπαγωγής 11 mH
• Αντίσταση 10 Ω
• Παλμογράφος Δυο Καναλιών

Διαδικασία:

Συνδέουμε σε σειρά το πηνίο, την αντίσταση και το τροφοδοτικό εναλλασσόμενης τάσης. Συνδέουμε το Κανάλι 1 του παλμογράφου στα άκρα της αντίστασης και το Κανάλι 2 στα άκρα του πηνίου. Τροφοδοτούμε το κύκλωμα με ημιτονοειδές σήμα με την βοήθεια της παλμογεννήτριας. Ρυθμίζουμε τον παλμογράφο ώστε να απεικονίζονται στην οθόνη του το Channel 1 και το Channel 2 ταυτόχρονα. Παρατηρούμε ότι οι δυο κυματομορφές δεν ταυτίζονται αλλά έχουν μια διαφορά φάσης η οποία είναι ίση με 90^ο, δηλαδή όταν η μια έχει μέγιστο η άλλη έχει ελάχιστο.

Γιατί συμβαίνει αυτό;

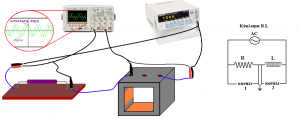
Εξήγηση:

Ας θεωρήσουμε ότι η παλμογεννήτρια μας, μας τροφοδοτεί με ημιτονοειδές σήμα της μορφής $V=V₀ημωt$.

Όταν στα άκρα της παλμογεννήτριας συνδέουμε ένα πηνίο εμφανίζεται εναλλασσόμενη μαγνητική ροή, η οποία δημιουργεί εναλλασσόμενη ΗΕΔ από αυτεπαγωγή, ίση και αντίθετη προς την ΗΕΔ της γεννήτριας. Η μαγνητική ροή είναι ανάλογη προς το ρεύμα και βρίσκεται στην ίδια με το ρεύμα φάση. Αν το ρεύμα και η ροή παριστάνονται από τις συναρτήσεις  και  η ΗΕΔ από αυτεπαγωγή V_L είναι ανάλογη προς το ρυθμό μεταβολής της ροής. Ο ρυθμός μεταβολής παριστάνεται από συνημιτονοειδές κύμα, δηλαδή κύμα μετατοπισμένο κατά π/2. Το αρνητικό μέγιστο σημειώνεται, όταν μηδενίζονται το ρεύμα και η ροή, λόγω του νόμου του Lenz. Αν Ν είναι ο αριθμός των σπειρών του πηνίου, η V_L εκφράζεται: $V_{L}=((NdΦ)/(dt))=L((dI)/(dt))=-LI₀(dημωt/dt)=-ωLI₀συνωt=V_{L0}ημ(ωt-(π/2))$ όπου $V_{L0}=ωLI₀=Z_{L}I₀$ και $Z_{L}=ωL$ είναι η επαγωγική αντίσταση.

Από τα προηγούμενα συμπεραίνουμε ότι το ρεύμα και κατά συνέπεια η τάση του πηνίου είναι ένα ημιτονοειδές κύμα που υστερεί από τη τάση της παλμογεννήτριας κατά 90^ο. Σε ένα κύκλωμα το οποίο αποτελείται από αντίσταση R και πηνίο L σε σειρά, η τάση του πηνίου υστερεί της τάση της παλμογεννήτριας κατά 90^ο και η σύνθετη αντίσταση του κυκλώματος είναι $Z_{RL}=\sqrt{R²+(ωL)²}$.