Διάταξη:

• Παλμογεννήτρια
• Πυκνωτής χωρητικότητας 10 μF
• Αντίσταση 1 ΚΩ
• Παλμογράφος Δυο Καναλιών

Διαδικασία:
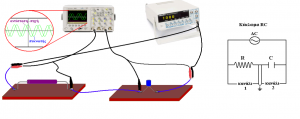
Συνδέουμε σε σειρά τον πυκνωτή, την αντίσταση και το τροφοδοτικό εναλλασσόμενης τάσης. Συνδέουμε το Κανάλι 1 του παλμογράφου στα άκρα της αντίστασης και το Κανάλι 2 στα άκρα του πυκνωτή. Τροφοδοτούμε το κύκλωμα με ημιτονοειδές σήμα με την βοήθεια της παλμογεννήτριας. Ρυθμίζουμε τον παλμογράφο ώστε να απεικονίζονται στην οθόνη του το Κανάλι 1 και το Κανάλι 2 ταυτόχρονα. Παρατηρούμε ότι οι δυο κυματομορφές δεν ταυτίζονται αλλά έχουν μια διαφορά φάσης η οποία είναι ίση με 90^ο, δηλαδή όταν η μια έχει μέγιστο η άλλη έχει ελάχιστο.
Γιατί συμβαίνει αυτό;

Εξήγηση:

Ας θεωρήσουμε ότι η παλμογεννήτρια μας, μας τροφοδοτεί με ημιτονοειδές σήμα της μορφής $V=V₀ημωt$. Όταν στα άκρα της συνδέουμε μια αντίσταση τότε από τον 2^ο νόμο του Kirchhoff προκύπτει: $V-IR=0⇒V₀ημωt-IR=0$ Το ρεύμα που διαρρέει την αντίσταση είναι:  $I(t)=(V₀/R)ημωt-I₀ημωt$ Συμπεραίνουμε ότι το ρεύμα και κατά συνέπεια η τάση της αντίστασης βρίσκεται σε φάση με την τάση της παλμογεννήτριας.

Όταν στα άκρα της παλμογεννήτριας συνδέουμε έναν πυκνωτή ο 2^ος νόμος του Kirchhoff γράφεται ως εξής: $V-V_{c}=0⇒V-(q/C)=0$.Οπότε το φορτίο εκφράζεται ως: $q(t)=V₀Cημωt$ Ενώ το ρεύμα είναι: $I(t)=((dq(t))/(dt))=C(dV/dt)=V₀Cωσυνωt=I₀ημ(ωt+(π/2))$.Όπου $I₀=V₀Cω=(V₀/1/Cω)=(V₀/(Z_{c})$ και $Z_{c}=(1/Cω)$ είναι η χωρητική αντίσταση. Συμπεραίνουμε ότι το ρεύμα και κατά συνέπεια η τάση του πυκνωτή παριστάνονται από ημιτονοειδές κύμα που προηγείται της τάση της παλμογεννήτριας κατά 90^ο. Η τάση γίνεται μέγιστη μετά από ένα τέταρτο της περιόδου μετά τη μέγιστη τιμή της τάσης της παλμογεννήτριας.

Σε ένα κύκλωμα το οποίο αποτελείται από αντίσταση R και πυκνωτή C σε σειρά, η τάση του πυκνωτή προηγείται της τάση της παλμογεννήτριας κατά 90^ο και η σύνθετη αντίσταση του κυκλώματος είναι: $Z_{RC}=√R²+(1/(Cω))²$