Διάταξη:

• Γεννήτρια παραγωγής ημιτονοειδούς κίνησης
• Οριζόντια χορδή μήκους 40 cm τα άκρα της οποίας είναι  στερεωμένα από την μία στη γεννήτρια και από την άλλη σε τροχαλία στην οποία είναι αναρτημένο κατάλληλο βάρος για τη δημιουργία τάσης.
• 

Διαδικασία:

• Ενεργοποιήστε τη γεννήτρια παραγωγής ημιτονοειδών κυμάτων μετακινώντας το διακόπτη  S₂ δεξιά και τον διακόπτη S₃ στη θέση α.
• Ρυθμίστε τη συχνότητα στα 10 Ηz και αυξήστε το πλάτος (amplitude). Παρατηρούμε ότι στην χορδή δημιουργείται στάσιμο κύμα. Τα άκρα της χορδής παραμένουν ακίνητα ενώ το μέσο ταλαντώνεται με το μέγιστο πλάτος. Γιατί συμβαίνει αυτό;
• Ρυθμίστε τη συχνότητα στα 20 Ηz και αυξήστε το πλάτος (amplitude). Παρατηρούμε ότι τρία σημεία της χορδής παραμένουν ακίνητα ενώ δύο ταλαντώνονται με το μέγιστο πλάτος. Γιατί συμβαίνει αυτό;
• Ρυθμίστε τη συχνότητα στα 30 Ηz και αυξήστε το πλάτος (amplitude). Παρατηρούμε ότι τέσσερα σημεία της χορδής παραμένουν ακίνητα ενώ τρία ταλαντώνονται με το μέγιστο πλάτος. Γιατί συμβαίνει αυτό;
• Ρυθμίστε τη συχνότητα στα 40 Ηz και αυξήστε το πλάτος (amplitude). Παρατηρούμε ότι πέντε σημεία της χορδής παραμένουν ακίνητα ενώ τέσσερα ταλαντώνονται με το μέγιστο πλάτος. Γιατί συμβαίνει αυτό;

Εξήγηση:

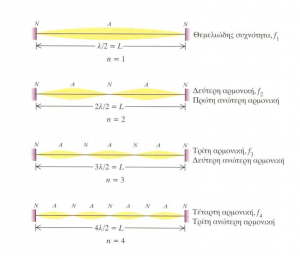
Όταν παράγουμε ένα ημιτονοειδές κύμα σε χορδή καθορισμένου μήκους L, με ακλόνητα και τα δύο άκρα, το κύμα ανακλάται και ξανά-ανακλάται στα άκρα. Τα κύματα συνδυάζονται για να σχηματίσουν στάσιμα κύματα μόνο όταν το μήκος L της χορδής είναι ακέραιο πολλαπλάσιο του λ/2, όπου λ είναι το μήκος κύματος. Δηλαδή $L=n\frac{\lambda}{2}$  (n=1, 2, 3…).  Τα σημεία τα οποία δεν κινούνται λέγονται κόμβοι (ή δεσμοί), ενώ μεταξύ αυτών υπάρχουν σημεία καλούμενα κοιλίες (αντιδεσμοί) όπου το πλάτος της κίνησης είναι μέγιστο. Οι αντίστοιχες επιτρεπτές συχνότητες είναι $f_{n}=n\frac{\upsilon}{2L}=nf_{1}$ (n=1, 2, 3…) όπου υ είναι η ταχύτητα του κύματος. Η μικρότερη συχνότητα  αντιστοιχεί στο μεγαλύτερο μήκος κύματος (n=1) και ονομάζεται θεμελιώδης συχνότητα. Οι άλλες συχνότητες είναι όλες ακέραια πολλαπλάσια της  και ονομάζονται αρμονικές και η σειρά ονομάζεται αρμονική σειρά.