Διάταξη:

• Πηγή φωτός laser Ηλίου-Νέου (He-Ne) ακτινοβολίας 633 nm και μέγιστης ισχύος 1 mW
• Μεταλλική Βάση
• 2 φιλμ με απλή και διπλή σχισμή
• Βαθμονομημένη Τροχιά
• Βαθμονομημένη οθόνη

Διαδικασία πειράματος απλής σχισμής:

Τοποθετούμε στην μεταλλική βάση το φιλμ με την απλή σχισμή, εύρους α = 0,1 mm. Ευθυγραμμίζουμε την πηγή laser και την μεταλλική βάση, πάνω στην τροχιά, έτσι ώστε η ακτίνα του laser να προσπίπτει συμμετρικά πάνω στη σχισμή. Παρατηρούμε ότι στην οθόνη παρουσιάζονται φωτεινοί και σκοτεινοί κροσσοί.

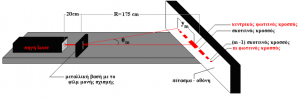
Εξήγηση:

Όταν μια ακτίνα φωτός προσπίπτει πάνω σε σχισμή εύρους α τότε εμφανίζεται το φαινόμενο της περίθλασης, σε οθόνη που απέχει απόσταση R από τη σχισμή. Σύμφωνα με την θεωρία η συνθήκη για την εμφάνιση ενός σκοτεινού κροσσού είναι $a\sin\vartheta=m\lambda~m=0,\pm1,\pm2\pm3…$

Για $R>>a~\sin\vartheta\approx\vartheta=\frac{m\lambda}{a}$ και $\sin\vartheta=\frac{y_{m}}{R}$ οπότε $y_{m}=\frac{m\lambda R}{a}$ όπου y_m η απόσταση του σκοτεινού κροσσού m τάξης από το κέντρο της εικόνας περίθλασης. Από τα δεδομένα της διάταξης μας, επαληθεύουμε το μήκος της σχισμής (για m = 1) $y_{m}=\frac{m\lambda R}{a}\Rightarrow a=\frac{m\lambda R}{y_{m}}\Rightarrow a=\frac{1\cdot633~10^{-9}m\cdot175~10^{-2}m}{1,1~10^{-2}m}\Rightarrow a=0,1mm$

Διαδικασία πειράματος διπλής σχισμής:

Τοποθετούμε στην μεταλλική βάση το φιλμ με τη διπλή σχισμή, εύρους   α = 0,1 mm η κάθε μια και απόστασης μεταξύ των σχισμών d = 0,5 mm. Ευθυγραμμίζουμε την πηγή laser και την μεταλλική βάση, πάνω στην τροχιά, έτσι ώστε η ακτίνα του laser να προσπίπτει ομοιόμορφα πάνω στη σχισμή. Παρατηρούμε ότι στην οθόνη παρουσιάζονται φωτεινοί και σκοτεινοί κροσσοί.

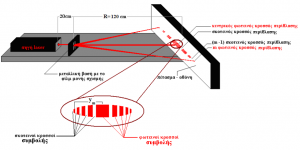
Εξήγηση:

Όταν μια ακτίνα φωτός προσπίπτει πάνω σε διπλές σχισμές, εύρους         α = 0,1 mm η κάθε μια και απόστασης μεταξύ των σχισμών d = 0,5 mmτότε εμφανίζεται το φαινόμενο της περίθλασης σε κάθε σχισμή και το φαινόμενο της συμβολής μεταξύ των ακτινών που φεύγουν από τις σχισμές, σε οθόνη που απέχει απόσταση R από τη σχισμή. Οι λεπτοί κροσσοί οφείλονται στη συμβολή των κυμάτων και οι πλατιοί κροσσοί οφείλονται στην περίθλαση των κυμάτων. Σύμφωνα με την θεωρία η συνθήκη για την εμφάνιση ενός φωτεινού κροσσού συμβολής είναι $a\sin\vartheta=m\lambda~m=0,\pm1,\pm2\pm3…$

Για $d,a<<R$ είναι $\sin\vartheta=\frac{y_{m}}{R}\Rightarrow y_{m=}\frac{m\lambda R}{d}$. Από τα δεδομένα της διάταξης μας, επαληθεύουμε την απόσταση των σχισμών $y_{m=}\frac{m\lambda R}{d}\Rightarrow d=\frac{m\lambda R}{y_{m}}\Rightarrow d=\frac{4\cdot633~10^{-9}m\cdot120~10^{-2}m}{0,6~10^{-2}m}\Rightarrow d=0,5mm$