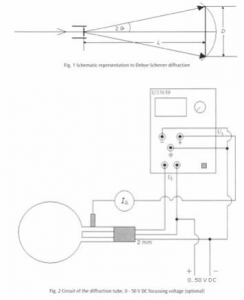
Η λυχνία περίθλασης ηλεκτρονίων επιδεικνύει την κυματική φύση των σωματίων αυτών, επιτρέποντας την παρατήρηση της συμβολής σε φθορίζουσα οθόνη, δέσμης ηλεκτρονίων η οποία προσπίπτει πάνω σε λεπτό πολυκρυσταλλικό δείγμα γραφίτη. Η γεωμετρία που χρησιμοποιεί η συγκεκριμένη συσκευή είναι γνωστή ως περίθλαση Debye – Scherrer.

Περιγραφή της αρχής Λειτουργίας:

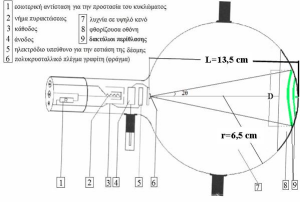
Η συσκευή μας έχει σαν βασικά εξαρτήματα της μια λυχνία, εντός της οποίας υπάρχει υψηλό κενό και θερμαινόμενο νήμα πυρακτώσεως βολφραμίου, που τροφοδοτεί την λυχνία με ηλεκτρόνια. Τα ηλεκτρόνια προκύπτουν καθώς το νήμα πυρακτώνεται με την συνδρομή της καθόδου αποκτώντας μορφή λεπτής δέσμης και επιταχύνονται από την άνοδο μετά την διέλευση τους από διάφραγμα και κατόπιν εστιάζονται με την βοήθεια ειδικού ηλεκτροδίου. Η δέσμη λεπτή, εστιασμένη και σχεδόν μονοχρωματική, οδηγείται στο χώρο όπου υπάρχει λεπτό υμένιο (αποτελείται από μερικά ατομικά στρώματα) πολυκρυσταλλικού γραφίτη.

Το υμένιο γραφίτη δρα σαν φράγμα περίθλασης με συνέπεια η δέσμη να περιθλάται όταν προσπέσει σ’ αυτό.

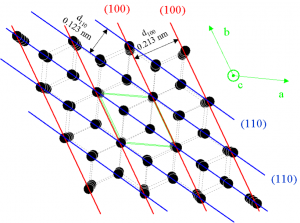
Το αποτέλεσμα είναι δύο ομόκεντροι δακτύλιοι περίθλασης οι οποίοι γίνονται ορατοί στην φθορίζουσα οθόνη της λυχνίας. Στο κέντρο των ομόκεντρων δακτυλίων παρατηρείται σχεδόν ‘σημειακό’ φθορίζων σήμα το οποίο απεικονίζει το μέρος της δέσμης που δεν περιθλάστηκε. Τα στοιχειώδη σωμάτια, όπως τα ηλεκτρόνια, έχουν δυική υπόσταση, μπορούν δηλαδή να εμφανιστούν ή να παρασταθούν και ως σωμάτια αλλά και ως κύματα. Πρώτος ο deBroglie διατύπωσε αυτή τη θεωρία το 1926. Έτσι μια δέσμη ηλεκτρονίων μπορεί να χειρισθεί ως μια δέσμη κυμάτων τα οποία περιθλώνται από ένα πλέγμα ατόμων άνθρακα (γραφίτη). Το πλέγμα αυτό έχει εξαγωνική δομή όπως φαίνεται στην εικόνα και αποτελείται από διαδοχικά φύλλα εξαγωνικών δομών άνθρακα (γραφιτικά φύλα). Τα φύλλα αυτά είναι διατεταγμένα κατά τέτοιο τρόπο ώστε εκατέρωθεν του κέντρου κάθε εξαγώνου στο κάθε φύλλο βρίσκεται ένα άτομο άνθρακα από το επάνω και το κάτω από αυτό επόμενο φύλλο αντίστοιχα.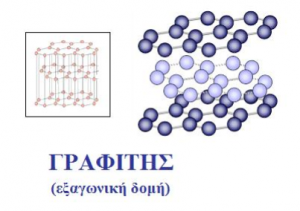

Τα κύματα των ηλεκτρονίων ανακλώνται από τα παράλληλα επίπεδα των ατόμων του γραφίτη και συμβάλλουν σε ορισμένα σημεία του χώρου. Η σχέση που μας δίνει την γωνιακή θέση θ των σημείων περίθλασης των κυμάτων από δυο παράλληλα ατομικά επίπεδα του γραφίτη είναι γνωστή ως νόμος του Bragg:

λ = 2dsinθ

όπου λ το μήκος κύματος των ηλεκτρονίων, dη απόσταση των παράλληλων επίπεδων  και θ η γωνία ανάκλασης.

Λόγω της κατασκευής του δείγματος ως λεπτό υμένιο (thinfilm) μερικών ατομικών επιπέδων, τα γραφιτικά φύλλα έχουν στατιστικά έναν προτιμητέο προσανατολισμό στον χώρο, με αποτέλεσμα η περίθλαση να συμβαίνει κυρίως μόνο από δύο οικογένειες διαφορετικών επιπέδων, την (100) και την (110), οι οποίες φαίνονται στο παρακάτω σχήμα.

Επιπλέον λόγω της πολυκρυσταλλικής φύσης του δείγματος το σχήμα περίθλασης της δέσμης ηλεκτρονίων προκύπτει ότι είναι ένας κώνος με κορυφή το δείγμα γραφίτη και άξονα συμμετρίας την διεύθυνση της αρχικής μη περιθλώμενης δέσμης. Έτσι στην φθορίζουσα οθόνη παρατηρούμε την τομή των κώνων περίθλασης από τα επίπεδα (100) και (110) με την σφαιρική επιφάνεια της λυχνίας. Η γωνία του κώνου περίθλασης ως προς τον άξονα συμμετρίας του είναι ίση με 2θ. Η γωνία αυτή μπορεί να υπολογιστεί γεωμετρικά μετρώντας την διάμετρο Dτων δακτυλίων περίθλασης. και λαμβάνοντας υπ’ όψη τα τεχνικά χαρακτηριστικά της συσκευής. Από την γωνία αυτή μέσω της εξίσωσης του νόμου του Braggμπορεί να υπολογιστεί το μήκος κύματος λ των ηλεκτρονίων χρησιμοποιώντας τις γνωστές αποστάσεις dτων ατομικών επιπέδων του γραφίτη d₁₀₀=0.213 nm και d₁₁₀=0.123 nm:

λ=2d₁₀₀sin2θ₁ και λ=2d₁₁₀sin2θ₂

Πειραματική διαδικασία:

Συνδέστε την λυχνία με το τροφοδοτικό όπως δείχνει το σχήμα. Εφαρμόστε το δυναμικό χαμηλής τάσης (6.3 V) στον θερμαντήρα για ένα λεπτό έτσι ώστε να επιτευχθεί θερμοκρασιακή σταθερότητα. Αυξήστε την υψηλή τάση αργά εωσότου αυτή να ανέλθει στην τιμή των V=4.00 kV. Προσοχή, η ένταση του ρεύματος στο αμπερόμετρο δεν πρέπει να υπερβεί τα 0.2 mA και το λεπτό υμένιο γραφίτη θα πρέπει να παρατηρείται συχνά έτσι ώστε σε περίπτωση που παρατηρηθεί αναλαμπή του, κάτι που σημαίνει ότι αυτό θα έχει υπερθερμανθεί και κινδυνεύει να καταστραφεί, η συσκευή πρέπει αμέσως να αποσυνδεθεί από την παροχή ρεύματος.

Παρατηρήστε ότι ήδη από την τιμή V=3.00 kVαρχίζουν να εμφανίζονται δακτύλιοι περίθλασης οι οποίοι γίνονται αρκετά ευκρινής, αλλά και μικρότεροι σε διάμετρο, σε υψηλότερη τάση. Αυτό συμβαίνει γιατί το μήκος κύματος deBroglieτων ηλεκτρονίων εξαρτάται από την ορμή τους μέσω της σχέσης λ=h/p, όπου hη σταθερά του Plankκαι p η ορμή. Η ορμή αυξάνει με την αύξηση του δυναμικού επιτάχυνσης των ηλεκτρονίων, με αποτέλεσμα το μήκος κύματός τους να γίνεται μικρότερο και οι δακτύλιοι μέσω της σχέσης του νόμου του Braggνα εμφανίζονται σε μικρότερες γωνιακές θέσεις. Για σταθερή υψηλή τάση V=4.00 kV μετρήστε τις αποστάσεις Dτων δακτυλίων περίθλασης. Υπολογίστε τις γωνίες 2θ1 και 2θ2* από τα Dκαι Lκαι μέσω της σχέσης του νόμου του Bragg προσδιορίστε το μήκος κύματος των ηλεκτρονίων.

* Από τα γεωμετρικά χαρακτηριστικά της συσκευής σε καλή προσέγγιση  και για μικρές γωνίες 2θ μία καλή προσέγγιση του tan2θ είναι το 2sinθ, οπότε ο νόμος του Braggμας δίνει λ=2dsinθ»dD/2L.