Διάταξη:

• απλό εκκρεμές
• χρονόμετρο

Διαδικασία:

•  Απομακρύνετε το εκκρεμές από τη θέση ισορροπίας σε γωνία θ ≤ 5° και αφήστε το ελεύθερο.
•  Μετά από 1-2 πλήρεις αιωρήσεις μετρήστε με το χρονόμετρο χειρός το χρόνο δέκα πλήρων αιωρήσεων (t =10T) που κάνει το εκκρεμές.
•  Υπολογίστε την περίοδο της ταλάντωσης του εκκρεμούς από τη σχέση:
  Τ = Συνολικός χρόνος 10 αιωρήσεων /10
•  Υπολογίστε την επιτάχυνση βαρύτητας g.

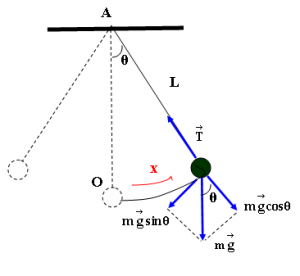
Απλό εκρεμμές

 Εξήγηση:
Το απλό εκκρεμές είναι ένα ιδανικό σύστημα που αποτελεί βασική εφαρμογή της απλής αρμονικής ταλάντωσης. Αποτελείται από μια σημειακή μάζα m κρεμασμένη μ’ ένα μη εκτατό και αβαρές νήμα μήκους L από ένα σταθερό σημείο. Όταν το απλό εκκρεμές απομακρυνθεί από τη θέση ισορροπίας κατά μικρή γωνία θ και αφεθεί ελεύθερο, αρχίζει να αιωρείται σε κατακόρυφο επίπεδο εκτελώντας απλή αρμονική κίνηση.
Το σχήμα δείχνει ένα απλό εκκρεμές που σχηματίζει γωνία θ με την κατακόρυφη. Η κατακόρυφη διεύθυνση ΑΟ είναι η θέση ισορροπίας ή

ελάχιστης δυναμικής ενέργειας του εκκρεμούς. Η κίνηση του εκκρεμούς οφείλεται στις δυνάμεις που δρουν πάνω στη μάζα m.
Οι ακτινικές συνιστώσες των δυνάμεων δίνουν την αναγκαία κεντρομόλο επιτάχυνση για να κινείται το σώμα πάνω στο τόξο του κύκλου με ακτίνα L και κέντρο το σημείο εξάρτησης Α. Η εφαπτομενική συνιστώσα είναι η δύναμη επαναφοράς (mgsinθ) που δρα πάνω στη μάζα m και τείνει να την ξαναφέρει στη θέση ισορροπίας. Αν θ < 5°, τότε sinθ ~ θ ~ x/L και η δύναμη επαναφοράς παίρνει τη μορφή:

$F\approx -mg\theta \approx -mg\frac{x}{L}=-kx$

με την σταθερά $k=\frac{mg}{L}$

 Στην απλή αρμονική ταλάντωση η περίοδος Τ δίνεται από τη σχέση:

$T=2\pi \frac{\sqrt{m}}{k}$

άρα, η περίοδος της ταλάντωσης ενός απλού εκκρεμούς, με μικρό πλάτος αιώρησης δίνεται από τη σχέση:

$T=2\pi \sqrt{\frac{L}{g}}\Rightarrow g=\frac{4\pi ^{2}L}{T^{2}}$

η οποία είναι ανεξάρτητη της μάζας m για μικρά πλάτη και επίσης ανεξάρτητη του πλάτους της ταλάντωσης. Συνεπώς, οι αιωρήσεις ενός απλού εκκρεμούς είναι ισόχρονοι, έστω και αν οι δυνάμεις απόσβεσης (αντίσταση του αέρα, τριβή στο σημείο εξάρτησης) ελαττώνουν βαθμιαία το πλάτος.