Διαδικασία:
- Η συσκευή περιστροφικής ταλάντωσης αποτελείται από οριζόντια ράβδο πάνω στην οποία μπορούν να μετακινηθούν δυο σώματα μάζας m το καθένα, εκατέρωθεν του σημείου στήριξης της ράβδου σε κατακόρυφο άξονα.
- Στην οριζόντια ράβδο της συσκευής μας τοποθετούμε τα δυο σώματα, στις δυο πιο κοντινές θέσεις που ισαπέχουν από τον κατακόρυφο άξονα περιστροφής.
- Στρέφουμε την οριζόντια ράβδο κατά 180ο και την αφήνουμε.
- Καταγράφουμε με το χρονόμετρο την περίοδο ταλάντωσης της ράβδου.
- Τοποθετούμε τα σώματα σε δυο συμμετρικές θέσεις μεγαλύτερης απόστασης από τον άξονα περιστροφής.
- Στρέφουμε πάλι την ράβδο κατά 180ο, την αφήνουμε και καταγράφουμε την νέα περίοδο ταλάντωσης της ράβδου.
- Τέλος τοποθετούμε τα σώματα στις πιο ακραίες θέσεις.
- Στρέφουμε την ράβδο κατά 180ο, την αφήνουμε και καταγράφουμε την περίοδο ταλάντωσης της ράβδου.
- Τι παρατηρούμε; Γιατί συμβαίνει αυτό;
Εξήγηση:
Με μια προσεκτικότερη ματιά της συσκευής μας, παρατηρούμε ότι στην βάση αυτής υπάρχει ένα περιτυλιγμένο ελατήριο. Όταν η ράβδος περιστραφεί κατά γωνία θ, ασκείται πάνω της μια ροπή επαναφοράς τ η οποία τείνει να περιστρέψει το σώμα με φορά αντίθετη από την αρχική γωνιακή μετατόπιση. Η ροπή αυτή δεν έχει σταθερό μέτρο αλλά είναι ανάλογη της γωνίας εκτροπής θ από την θέση ισορροπίας, τ=Dxθ όπου D σταθερά. Όταν η ράβδος αφεθεί ελεύθερη, ταλαντώνεται γύρω από την θέση ισορροπίας της.
Η εξίσωση περιστροφικής κίνησης της ράβδου είναι Στ = Ι α όπου Ι είναι η ροπή αδράνειας της ράβδου και των σωμάτων που βρίσκονται πάνω της ως προς τον κατακόρυφο άξονα περιστροφής και α η γωνιακή επιτάχυνση.
Βρίσκουμε ότι $-D\times\vartheta=Ia=I\frac{d^{2}\vartheta}{dt^{2}}$ οπότε $\frac{d^{2}\vartheta}{dt^{2}}=-\frac{-D\times\vartheta}{I}$ Συγκρίνοντας την παραπάνω σχέση με την αντίστοιχη εξίσωση της απλής αρμονικής κίνησης, $\frac{d^{2}x}{dt^{2}}=-\omega^{2}x$ συμπεραίνουμε ότι η γωνιακή συχνότητα δίνεται από την σχέση $\omega=\sqrt{\frac{D}{I}}$ και η περίοδος από την $T=2\pi\sqrt{\frac{I}{D}}$ (1). Παρατηρούμε δηλαδή ότι η περίοδος ταλάντωσης του συστήματος μας είναι ανάλογη του $I^{1/2}$. Η ροπή αδρανείας είναι ένα μέγεθος που μετρά την αδράνεια που επιδεικνύει ένα σώμα όταν μια ροπή αλλάζει την περιστροφική του κατάσταση.
Για το σύστημα μας η ροπή αδρανείας του είναι το άθροισμα της ροπής αδρανείας της ράβδου και των ροπών αδρανείας των σωμάτων. Δηλαδή η ροπή αδρανείας Ι του συστήματος είναι $I=I_{PAB}+2I_{MAZ}$ οπότε $I=\frac{1}{12}ML^{2}+2mr^{2}$
Όπου, Μ : η μάζα της ράβδου , L : το μήκος της ράβδου, m : η μάζα κάθε σώματος, r : η απόσταση κάθε σώματος από τον άξονα περιστροφής. Άρα η περίοδος του συστήματος είναι $T=2\pi\sqrt{\frac{\frac{1}{12}ML^{2}+2mr^{2}}{D}}$ (2)
Από την σχέση (2) συμπεραίνουμε ότι η περίοδος του συστήματος εξαρτάται από την θέση των σωμάτων πάνω στην οριζόντια ράβδο. Πράγματι, όσο απομακρύνουμε τα σώματα από τον άξονα περιστροφής παρατηρούμε να μεγαλώνει η περίοδος ταλάντωσης του συστήματος μας.
Ποσοτικός προσδιορισμός της σχέσης (1)
Με δεδομένες τις μάζες της ράβδου και των σωμάτων εκτελούμε έναν πειραματικό προσδιορισμό της περιόδου ταλάντωσης σαν συνάρτηση της απόστασης r. Η σταθερά D προσδιορίζεται από την μέτρηση της περιόδου ταλάντωσης της ράβδου χωρίς τα σώματα. Οι θεωρητικές τιμές του Τ προσδιορίζονται από την σχέση (1) θεωρώντας τα σώματα ως σημειακές μάζες.
| r (m) | I (kg·m2) | D (kg·m2/s2) | I1/2 (kg·m2)1/2 | Tθεωρητικό (s) | Tπειραματικό (s) |
| 0 | 0,0075 | 0,0462 | 0,0868 | 3,02 | 2,53 |
| 0,05 | 0,0087 | 0,0934 | 3,24 | 2,82 | |
| 0,1 | 0,0122 | 0,1107 | 3,85 | 3,87 | |
| 0,15 | 0,0182 | 0,1347 | 4,68 | 4,78 | |
| 0,2 | 0,0264 | 0,1625 | 5,64 | 6,00 | |
| 0,25 | 0,0370 | 0,1924 | 6,68 | 7,18 | |
| 0,3 | 0,0500 | 0,2236 | 7,77 | 8,59 |
από τα παραπάνω δεδομένα σχηματίσαμε τις παρακάτω γραφικές παραστάσεις
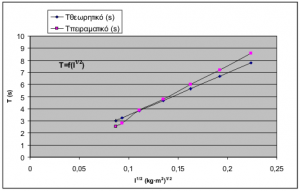
όπου πράγματι φαίνεται ότι η περίοδος της ταλάντωσης είναι ανάλογη του Ι½ και ότι οι πειραματικές μας τιμές συμφωνούν αρκετά καλά με την θεωρία.