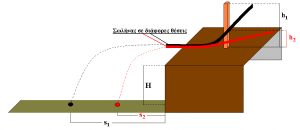
Διάταξη:
Η συσκευή αποτελείται από έναν σωλήνα του οποίου το ένα άκρο μπορεί να τοποθετηθεί σε διαφορετικά ύψη. Όταν αφήσουμε μια σφαίρα μάζας m να κυλήσει στο εσωτερικό του ξεκινώντας με μηδενική ταχύτητα, τότε η σφαίρα εξέρχεται από το άλλο άκρο του με ταχύτητα υ. Το μέγεθος της ταχύτητας αυτής εξαρτάται από το ύψος h στο οποίο βρίσκεται το άλλο άκρο. Αν θεωρήσουμε ότι δεν υπάρχουν τριβές κατά την κίνηση της σφαίρας και ότι η κύλιση της σφαίρας απορροφά αμελητέο ποσό ενέργειας, τότε η ταχύτητα υ μπορεί να υπολογιστεί από την αρχή διατήρησης της ενέργειας.
Διαδικασία:
Η συσκευή με τον σωλήνα μας δίνει ένα χαρακτηριστικό παράδειγμα της μετατροπής της ενέργειας σε δυο από τις πιο συχνά εμφανιζόμενες στην καθημερινότητα μορφές της, την δυναμική και την κινητική. Όταν αφήνουμε την σφαίρα στο πάνω μέρος του σωλήνα έχει δυναμική ενέργεια ίση με mgh. Όταν η σφαίρα φτάνει στο κάτω άκρο του σωλήνα η δυναμική ενέργεια έχει μετατραπεί σε κινητική, και έτσι μπορούμε να υπολογίσουμε την ταχύτητα της.

$K_{\alpha \rho \chi }+U_{\alpha \rho \chi }=K_{\tau \varepsilon \lambda }+U_{\tau \varepsilon \lambda }$ $\Rightarrow mgh=\frac{1}{2}mu^{2}\Rightarrow u=\sqrt{2gh}$ (1)

Πέρα από το κατώτερο σημείο του σωλήνα η συσκευή μας δίνει την δυνατότητα να μελετήσουμε την οριζόντια βολή που εκτελεί η σφαίρα μέχρι να φτάσει στο πάτωμα.
Στην οριζόντια βολή ένα σώμα εκτελεί ευθύγραμμη (σχεδόν) ομαλή κίνηση ως προς τον οριζόντιο άξονα και (προσεγγιστικά) ελεύθερη πτώση ως προς τον κατακόρυφο άξονα.

Δηλαδή είναι $v_{0x}=v$ και $v_{0y}=0$ . Αν t είναι ο χρόνος που χρειάζεται η σφαίρα μετά την έξοδο της από τον σωλήνα για να πέσει στο πάτωμα, τότε: $s=\upsilon t$ $H=\frac{1}{2}gt^{2}\Rightarrow t=\sqrt{\frac{2H}{g}}$

οπότε  $s=\upsilon \sqrt{\frac{2H}{g}}$ και από την σχέση (1) $s=2\sqrt{H}\sqrt{h}$

Από τις παραπάνω σχέσεις προκύπτει ότι η οριζόντια απόσταση της βολής είναι ανάλογη της τετραγωνικής ρίζας του αρχικού ύψους h. Άρα για να διπλασιάσουμε την απόσταση βολής πρέπει να τετραπλασιάσουμε το αρχικό ύψος h, πράγματι έχουμε:

$ \left.\begin{array}{c} s_{1}=2\sqrt{H}\sqrt{h_{1}}\\ s_{2}=2\sqrt{H}\sqrt{h_{2}} \end{array} \right\}\Rightarrow\frac{s_{1}}{s_{2}}=\sqrt{\frac{h_{1}}{h_{2}}}\sqrt{\frac{4h_{2}}{h_{2}}}=2$

Παρατηρούμε ότι αν εκτελέσουμε το πείραμα με $h_{1}=4h_{2}$ δεν παίρνουμε ακριβώς $s_{1}=2s_{2}$. Γιατί συμβαίνει αυτό;

Εξήγηση:
Σε όλη την παραπάνω προσέγγιση θεωρήσαμε ότι είχαμε αμελητέες τριβές για την σφαίρα κατά την διάρκεια της κίνησης της μέσα στον σωλήνα και επίσης αγνοήσαμε την διαδικασία κύλισης της. Αυτοί οι δύο παράγοντες φαίνεται ότι παίζουν σημαντικό ρόλο στην διαμόρφωση της τελικής ταχύτητας μεταφοράς υ της σφαίρας στο σημείο εξόδου της από τον σωλήνα με αποτέλεσμα οι μετρήσεις μας να αποκλίνουν από τις θεωρητικά αναμενόμενες.